Question

How do you Find a formula for the inverse of the function. f(x) =4x−1/2x+3. f−1(x) =?

Answer 1

`f^(-1) (x)=(-3x-1)/(2x-4)`,
`x\\eq2`.

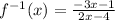Explanation:

1. Write the expression.

`f(x)=(4x-1)/(2x+3)`

2. Substitute "f(x)" by "y".

`y=(4x-1)/(2x+3)`

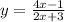
3. Swap places between y and x.

In other words, where there's "y", write "x"; where there's "x", write "y".

`x=(4y-1)/(2y+3)`

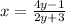
4. Multiply both sides of the equation by "2y+3".

`(2y+3)x=(4y-1)/(2y+3)*(2y+3)\\ \\(2y+3)x=4y-1}\\ \\2yx+3x=4y-1`

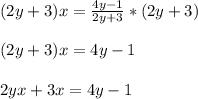
5.Subtract "3x" from both sides.

`2yx+3x-3x=4y-1-3x\\ \\2yx=4y-1-3x`

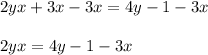
6. Subtract "4y" from both sides.

`2yx-4y=4y-1-3x-4y\\ \\2yx-4y=-3x-1\\ \\`

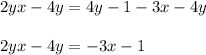
7. Factorize "2y".

`(2y)(x-2)=-3x-1\\\\2y=(-3x-1)/((x-2))`

8. Divide both sides by 2.

`(2y)/(2) =(-3x-1)/(2(x-2))\\ \\y=(-3x-1)/(2(x-2))\\ \\y=(-3x-1)/(2x-4)`

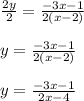
9. Express your result.

`f^(-1) (x)=(-3x-1)/(2x-4)`,
`x\\eq2`.

------------------------------------------------------------------------------------------------------------

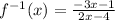Note: Since this is a reciprocal function, there are some values that cannot be evaluated through it. In this case, x=2 is one of those values. Hence, x=2 is an asymptote of this function.