An exponential function is defined by
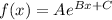
Where x occurs as an exponent.
The exponential curve depends on the exponential function and it depends on the value of the x. Where a>0 and a is not equal to 1. x is any real number.
If we graph the data table we can see that:
From the general equation we take the natural logarithm to both sides to be able to solve for A, B and C easily. With the points in the table we will make the different equations, as we have 3 unknowns we must have at least 3 equations
We can see graphically that there is no phase shift in the function, which is why C = 0

We have the values of x and F(x) from the tables, we are going to replace them to find the equations
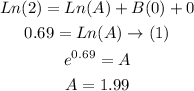


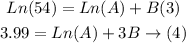
Now we have the 4 equations and we have 2 unknowns we will solve between them to find the values of A, B and C
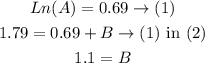
Then our equation would be:
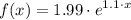
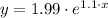
You can round the function as follows:
