We know that there are 26 letters and 10 digits to form each plate. Given that we need three letters and four digits, we have to elevate 26 to the third power and 10 to the fourth power because the product of these powers would be the solution.

Therefore, the total number of plates would be 175,760,000.
However, if the letter can't be repeated, then we have to calculate that part as follows

Then, we add them with the number of digits to get 156,000,000.
But, if we can repeat numbers, then we have to solve as follows
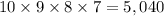
So, we have to multiply the number of combinations without repetition.

Therefore, the number of plates, without repetition, is 78,624,000.