1 Answer

Spacemigas · Answer 1 · 2023-06-21T08:28:48+0000

Given triangle is

Using the triangle sum property, we get

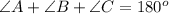
$\angle A+\angle B+\angle C=180^o$
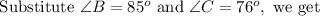
$\text{ Substitute }\angle B=85^o\text{ and }\angle C=76^o,\text{ we get}$
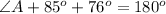
$\angle A+85^o+76^o=180^o$

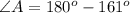
$\angle A=180^o-161^o$
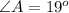
$\angle A=19^o$

Given a=1200 yards.

We need to find b and c.

Consider the sine law.

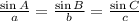
$(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)$

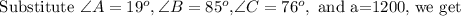
$\text{ Substitute }\angle A=19^o,\angle B=85^o\text{,}\angle C=76^o,\text{ and a=1200, we get}$

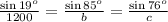
$(\sin 19^o)/(1200)=(\sin 85^o)/(b)=(\sin 76^o)/(c)$

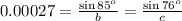
$0.00027=(\sin85^o)/(b)=(\sin76^o)/(c)$

Consider the following equation to find the value of b.

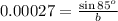
$0.00027=(\sin85^o)/(b)$

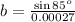
$b=(\sin 85^o)/(0.00027)$
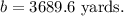
$b=3689.6\text{ yards.}$

Consider the following equation to find the value of c.

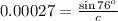
$0.00027=(\sin76^o)/(c)$

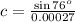
$c=(\sin 76^o)/(0.00027)$
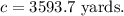
$c=3593.7\text{ yards.}$

Hence the distances of the oil platform from each end of the beach are 3689.6 yards and 3592.7 yards.

Please log in or register to add a comment.