Question

I need to know the answer this, please and thank you it’s past my bed time lol

Answer 1

To find the slope-intercept equation of a line, we need the slope (m) and the y-intercept (b).

The slope-intercept equation is noted as:

`y=mx+b`

To find the slope, we will use the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

Line 1:

The line passes through the points (-1, -4) and (1, 2). Using these points, we will solve the slope:

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ m=(2-(-4))/(1-(-1)) \\ m=(2+4)/(1+1) \\ m=(6)/(2)=3 \end{gathered}`

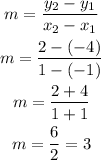
Then, using the point (-1, -4), we will solve for b:

`\begin{gathered} y=mx+b \\ -4=3(-1)+b \\ -4=-3+b \\ b=-4+3 \\ b=-1 \end{gathered}`

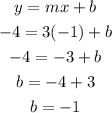
Now that we have the values of slope (m) and y-intercept (b), we now know that the slope-intercept form of line 1 is:

`\begin{gathered} y=mx+b \\ y=3x-1 \end{gathered}`

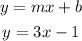
Line 2:

Following the same process, we will find the slope (m), then the y-intercept (b).

Line 2 passes through points (-4, 0) and (0,4)

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ m=(4-0)/(0-(-4)) \\ m=(4)/(0+4) \\ m=(4)/(4)=1 \end{gathered}`

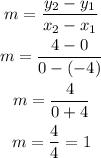
Then solve for the y-intercept (b) using the point (-4, 0):

`\begin{gathered} y=mx+b \\ 0=-4+b \\ b=4 \end{gathered}`

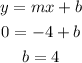
The equation would then be:

`\begin{gathered} y=mx+b \\ y=x+4 \end{gathered}`

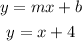
Line 3:

Line 3 passes through points (1, 0) and (0,2)

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ m=(2-0)/(0-1) \\ m=(2)/(-1)=-2 \end{gathered}`
`\begin{gathered} y=mx+b \\ 0=-2(1)+b \\ 0=-2+b \\ b=2 \end{gathered}`

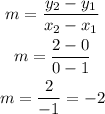
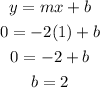
The equation then would be:

`\begin{gathered} y=mx+b \\ y=-2x+2 \end{gathered}`

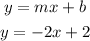
Line 4:

Line 4 passes through points (-2, 3) and (2, 1)

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ m=(1-3)/(2-(-2)) \\ m=(-2)/(4)=-(1)/(2) \end{gathered}`
`\begin{gathered} y=mx+b \\ 3=-(1)/(2)(-2)+b \\ 3=1+b \\ b=3-1 \\ b=2 \end{gathered}`

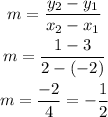
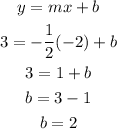
The equation is then:

`y=-(1)/(2)x+2`

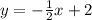
With all these, we can write each line's corresponding letter:

Line 1: A

Line 2: E

Line 3: B

Line 4: G