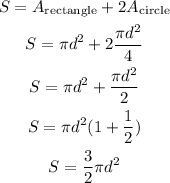Question

Create a cylinder that has the same diameter as the height. Find its surface area.

Answer 1

`S=(3)/(2)\pi d^2`

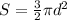
Step-by-step explanation

The surface area is the sum of the areas of the sides.

The areas of the top and the base are the areas of circles with diameter d:

`A_{\text{circle}}=\pi r^2=\pi\mleft((d)/(2)\mright)^2=(\pi d^2)/(4)`

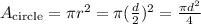
The area of the rest of the cylinder is the area of a rectangle, with height d and width the circumference of the circle:

`C=\pi d`
`A_{\text{rectangle}}=C\cdot d=\pi d^2`

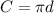
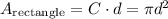
The surface area is:

`\begin{gathered} S=A_{\text{rectangle}}+2A_{\text{circle}} \\ S=\pi d^2+2(\pi d^2)/(4) \\ S=\pi d^2+(\pi d^2)/(2) \\ S=\pi d^2(1+(1)/(2)) \\ S=(3)/(2)\pi d^2 \end{gathered}`