ANSWER
• Solution: (4, -2)
,
• Graph: ,first equation in red and second equation in purple. Solution in orange.
Step-by-step explanation
The two equations in the system are linear equations, so their graphs are lines. The solution to the system is the point where the two lines intersect.
The first equation is in the slope-intercept form. The y-intercept is -1, and we can find the x-intercept by substituting y = 0,
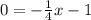
Solving for x,
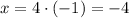
So, the line passes through the points (0, -1) and (-4, 0),
The second equation is in standard form. We can find the x and y-intercepts by substituting y and x with 0, respectively,
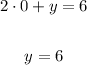

Thus, the y-intercept is (0, 6) and the x-intercept is (3, 0),
And the point where the two lines intersect is the solution,
Hence, the solution is (4, -2).