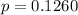Step 1
Given; The main cost of a 5 pound bag of shrimp is $47 with a variance of 36. If a sample of 43 bags of shrimp is randomly selected what is the probability that the sample mean would differ from the true mean by greater than $1.4? round your answer to four decimal places.
Step 2
In a set with mean and standard deviation, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
The Central Limit Theorem establishes that, for a random variable X, with mean and standard deviation, the sample means with size n of at least 30 can be approximated to a normal distribution with mean and standard deviation.
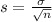
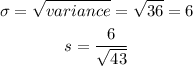
What is the probability that the sample mean would differ from the true mean by greater than 1.4 dollar?
x = 48.4
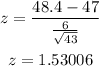
x=45.6
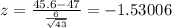

The difference will be;


Answer;