Question

Find the sum of the first 10 terms of the arithmetic sequence: 5, 12, 19, 26, ...

Answer 1

S₁₀ = 365

Step-by-step explanation

The sum of the first n terms of an arithmetic sequence is called the arithmetic series formula, given by,

`S_n=(n(a_1+a_n))/(2)`

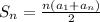
In this sequence, we can see that a₁ = 5, and the sum we have to find is the sum of the first 10 terms, so n = 10. To find the sum, we have to find the term a₁₀ first.

The nth term of an arithmetic sequence is given by the formula,

`a_n=a_1+d(n-1)`

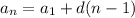
Where d is the common difference. To find this formula for this sequence, we have to find the common difference by using any of the given terms. If we use n = 2 - in other words, we write it for a₂,

`a_2=12=5+d(2-1)`

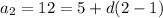
Solving for d,

`\begin{gathered} 12=5+d \\ d=12-5=7 \end{gathered}`

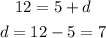
Thus, the formula for the nth term of this sequence is,

`a_n=5+7(n-1)`

And the 10th term is,

`a_(10)=5+7(10-1)=5+7\cdot9=5+63=68`

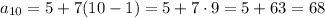
So, the sum of the first 10 terms is,

`S_(10)=(10(5+68))/(2)=(10\cdot73)/(2)=(730)/(2)=365`

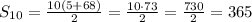
Hence, the sum of the first 10 terms of this arithmetic sequence is 365.