Algebraic expressions are given. It is required to tell if they are polynomials, tell how many terms they have, and give reasons if they are not a polynomial.
Recall that polynomials are a monomial or a sum of monomials.
Recall also that monomials are a number, a variable, or a product of numbers and variables with whole-number exponents.
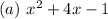
Notice that this satisfies the definition of a polynomial.
Hence, it is a polynomial and it has 3 terms.
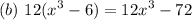
Notice that this satisfies the definition of a polynomial.
Hence, it is a polynomial and it has 2 terms.
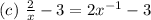
Notice that this expression does not satisfy the definition of a polynomial as it has a monomial with a negative number exponent variable, which is not a whole number.
Hence, it is not a polynomial, it has a term that has a variable with a negative exponent.
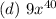
This is a polynomial with just 1 term.
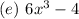
This satisfies the definition of a polynomial.
Hence, it is a polynomial and it has 2 terms.
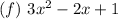
This also satisfies the definition of a polynomial as it only has monomials with variables of whole-number exponents.
Hence, it is a polynomial and it has 3 terms.
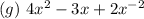
It is not a polynomial, it has a term that has a variable with a negative exponent.

This also satisfies the definition of a polynomial as it only has monomials with variables of whole-number exponents.
Hence, it is a polynomial and it has 4 terms.
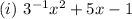
This also satisfies the definition of a polynomial as it only has monomials with variables of whole-number exponents.
Hence, it is a polynomial and it has 3 terms.