Given:
probability of success (p) = 7.3% or 0.073 in decimal form
sample size = 29
Find: the probability of x = 1 (uses public transportation on a regular basis)
Solution:
Based on the given information, the probability of success is only 7.3%. From this, we can infer that the probability of failure would be 92.7% or 0.927 in decimal form.
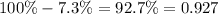
Since there are only two possible outcomes here, uses public transportation (success) and not using public transportation (failure), we are dealing with binomial probability.
The formula for this is:
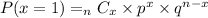
where n = sample size, x = the number of success, p = success probability, and q = failure probability.
In the word problem, n = 29, x = 1, p = 0.073, and q = 0.927. Let's plug this into the formula above.
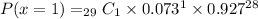
Then, solve.
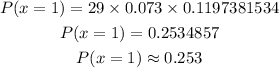
Answer:
The probability that exactly one of them uses public transportation on a regular basis is approximately 0.253.