Given:
Points and lie on the same line, as shown in the coordinate plane picture
The coordinates of point J = (3, 3.5)
The coordinates of point K = (6, 5)
We will answer the following questions:
) What is the slope of the line passing through points and ?
The slope is given by the formula:
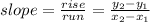
Substitute with the points J and K
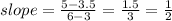
) Write the equation of the line passing through points and
The slope-intercept form of the equation is as follows

where m is the slope, and (b) is the y-intercept
So, from (A) m = 1/2
As shown in the figure, b = y-intercept = 2
So, the equation of the line will be:
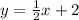
) Points and are added to the coordinate plane and a new line, , is made. Describe the three possible solutions to the system of linear functions, , and , made.
So, there are 3 possible solutions:
First, the line LM has a different slope, so, it will be consistent independent system, the lines will intersect at one point
Second, The lines have the same slope and the same y-intercepts, the system will be a consistent dependent system the lines will be identical (the same line), there are infinite solutions
Third, the lines have the same slope but a different y-intercept, the lines will be parallel, there is no intersection between them so, there is no solution, it will be an inconsistent system.