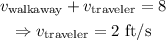Question

The travelers is on a airport moving walkway? the travelers ground speed is 4 ft/s against the walkway and 8ft/s with the walkway. what is the travelers speed off the walkway? what is the speed of the moving walkway?

Answer 1

Traveler's ground speed against the walkaway:

`v_{\text{against}}=4\text{ ft/s}`

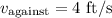
Traveler's ground speed with the walkaway:

`v_{\text{with}}=8\text{ ft/s}`

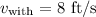
When the traveler is moving against the walkaway, the resulting speed is:

`v_{\text{against}}=|v_{\text{walkaway}}-v_{\text{traveler}}|`

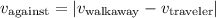
Where v_walkaway is the speed of the walkaway, and v_traveler is the traveler speed off the walkaway.

Similarly, if the traveler is moving with the traveler:

`v_{\text{with}}=v_{\text{walkaway}}+v_{\text{traveler}}`

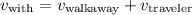
Then, the system of equations:

`\begin{gathered} 8=v_{\text{walkaway}}+v_{\text{traveler}} \\ 4=v_{\text{walkaway}}-v_{\text{traveler}} \end{gathered}`

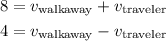
Adding these equations:

`\begin{gathered} 8+4=v_{\text{walkaway}}+v_{\text{traveler}}+v_{\text{walkaway}}-v_{\text{traveler}} \\ 2v_{\text{walkaway}}=12_{} \\ v_{\text{walkaway}}=6\text{ ft/s} \end{gathered}`

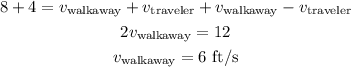
Using this value and the first equation:

`\begin{gathered} v_{\text{walkaway}}+v_{\text{traveler}}=8 \\ \Rightarrow v_{\text{traveler}}=2\text{ ft/s} \end{gathered}`