We have to find the probability that the point is in the smaller shaded square.
The probability of a point being located in the smaller square is equal to the ratio between the areas of the smaller square and the bigger square.
Then, we can express it as:
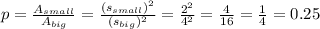
Answer: the probability tha the point falls in the smaller triangle is equal to 0.25.