For this problem, we need to explain why factoring a polynomial function might be necessary or useful.
One very useful piece of information about a polynomial is the points of its roots or zeros, these are the points that make the expression equal to 0. Let's take the following polynomial as an example:
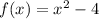
This polynomial has the following zeros: -2 and 2. If we factor this polynomial, we will arrive at the following conclusion:
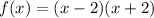
Notice how the factoring matches the zeros, but with opposite signs. This is true for any polynomial, if a polynomial of 4th degree has the roots a, b, c and d, it can be rewritten as:

For this reason, factoring a polynomial is very useful, because we can immediately determine its roots without making any calculation.