Question

For question 5 and question 6 calculate the missing y values in the table of the exponential function

Answer 1

In order to find the missing values in the table, let's use the following exponential model:

`y=a\cdot b^x`

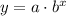
Now, to find the values of a and b, let's use the ordered pairs (0, 3) and (1, 15) from the table:

`\begin{gathered} (0,3)\colon \\ 3=a\cdot b^0 \\ a=3 \\ \\ (1,15)\colon \\ 15=3\cdot b^1 \\ b=(15)/(3)=5 \end{gathered}`

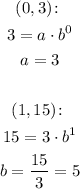
Therefore the equation is y = 3 * 5^x.

Now, using x = -1 and x = 3, we have:

`\begin{gathered} x=-1\colon \\ y=3\cdot5^(-1)=3\cdot(1)/(5)=(3)/(5) \\ \\ x=3\colon \\ y=3\cdot5^3=3\cdot125=375 \end{gathered}`

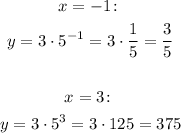
Therefore question 5 is equal to 3/5 and question 6 is equal to 375.