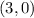
Step-by-step explanation
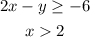
Step 1
graph the inequalities
a)
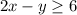
to graph this inequaliy, change the sign to make it an equation, and then isolate y
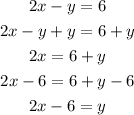
now ,get 2 coordinates
when x= 1
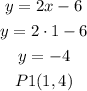
when x= 3
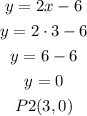
now, draw a line that passes trhough the points (1,4) and (3,0)
finally, return to the original sign,so
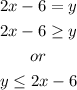
it means , we need all y smaller than the line( values under the line), so, it looks like this
Step 2
now , to graph
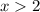
those are all x values greater than 2, ( to the rigth of 2)
graph both inequalities
finally, pick a point from the common zone
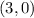
I hope this helps you