We are asked to use the logistic model to determine the population of plants given the constraints. The logistic growth model follows the next formula:
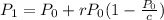
Where:
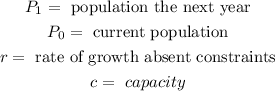
Now, we are given that the growth rate is 36%, this in decimal form is:
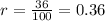
Now, we plug in the values:
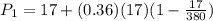
Solving the operations:
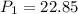
Therefore, the population next year is 22.85