we are given the functions
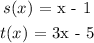
1. we are to find (s + t)(x)
given s(x) = x -1 and t(x) = 3x - 5 we have

Therefore, (s + t)(x) = 4x - 6
2. we are to find (s - t)(x)
using the functions s(x) and t(x), this will give
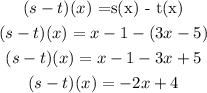
Therefore, (s - t)(x) = -2x + 4
3. we are to find (s.t)(2)
first we need to find
(s.t)(x)
using the functions s(x) and t(x) we have
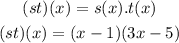
Therefore, (s.t)(x) = (x - 1)(3x - 5)
Hence

Therefore, (s.t)(2) = 1