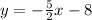Slope Intercept Form:

Where
m is slope
b is y-intercept (y-axis cutting point)
Now,
We know parallel lines have equal slope.
Let's work with the line equation given to find its slope:
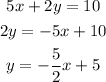
Slope is -5/2. This will be same for our line.
So, we can write:

To find b, we put (-6,7) into x and y respectively and find b:
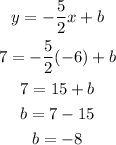
So, final equation: