Question

Find c.Write your answer in simplest radical form. ____ meters.

Answer 1

c= 5 meters

Step-by-step explanation

we have a rigth triangle, then

Step 1

Let

`\begin{gathered} \text{angle}=45\text{ \degree} \\ \text{hypotenuse}=5\sqrt[]{2} \\ \text{adjacent side= c} \end{gathered}`

hence, we need a function that relates: angle, adjacent side and hypotenuse

`\cos \text{ }\emptyset\text{= }\frac{adjacent\text{ side}}{\text{hypotenuse}}`

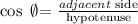
now, replace

`\begin{gathered} \cos \text{ }\emptyset\text{= }\frac{adjacent\text{ side}}{\text{hypotenuse}} \\ \cos \text{ 45= }\frac{c}{5\sqrt[]{2}} \end{gathered}`

Step 2

solve the equation

`\begin{gathered} \cos \text{ 45= }\frac{c}{5\sqrt[]{2}} \\ \frac{\sqrt[]{2}}{2}=\frac{c}{5\sqrt[]{2}} \\ \text{Multiply both sides by 5}\sqrt[]{2} \\ \frac{\sqrt[]{2}}{2}\cdot5\sqrt[]{2}=\frac{c}{5\sqrt[]{2}}\cdot5\sqrt[]{2} \\ (10)/(2)=c \\ 5=c \end{gathered}`

therefore, teh answer is

c=5 meters

I hope this helps you