Solution:
Given the system of equations below:
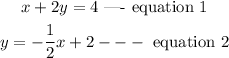
From equation, to graph equation 1, we solve for y for various values of x.
Thus,

By plotting the values of x and y as points (x, y), we have the graph of equation 1 to be
Similarly, from equation 2, the values of y for various values of x is thus
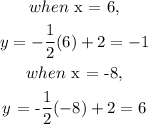
By plotting the values of x and y as points (x, y), we have the graph of equation 2 to be
By combining the graphs, we have infinitely many solutions.