Question

#1 Determine the constant of proportionality of the graph Money 376 Total Savings (9) Number of Weeks

Answer 1

The constant of proportionality is 47 dollars/week

`k=47\text{ dollars/week}`

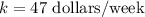
Step-by-step explanation:

From the graph;

The total savings (t) is directly proportional to the number of weeks (n).

`\begin{gathered} t\propto n \\ t=kn \\ k=(t)/(n) \\ k=(\Delta t)/(\Delta n) \end{gathered}`

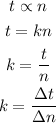
Where k is the constant of proportionality.

From the graph;

Total Savings starts from 0 and ends on 470 dollars

while the number of weeks starts from 0 to 10 weeks.

`\begin{gathered} k=(\Delta t)/(\Delta n)=(470-0)/(10-0)\text{ dollars/week} \\ k=(470)/(10)\text{ dollars/week} \\ k=47\text{ dollars/week} \end{gathered}`

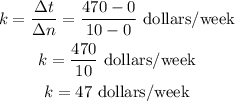
Therefore, the constant of proportionality is 47 dollars/week