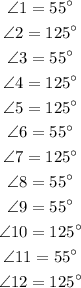Two angles are supplementary if the sum of its measure is 180°. Usually a pair of supplementary angles looks like this:
In the picture you can see that there are several cases like this. Another geometric property that we are going to use is related to the fact that lines l and m are parallel just like lines n and p. This means that the angles on one interception are exactly the same as those in any other interception. This means that:
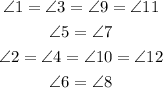
Using this, the measure of angle 1 and identifying supplementary angles we should be able to find the 11 remaining measures. So let's start.
As I stated before :

And since the measure of 1 is 55° then angles 3, 9 and 11 also have a measure of 55°.
If you look at the picture representing supplementary angles you can see that angles 1 and 2 are supplementary. This means that:
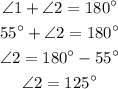
And since:
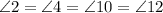
Then angles 2, 4, 10 and 12 all measure 125°.
Another pair of supplementary angles is 1 and 5. Repeating what we did with angles 1 and 2 we have that the measure of angle 5 is 125° and since:
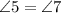
Then the measure of angle 7 is also 125°.
Angles 2 and 6 are also supplementary, then:
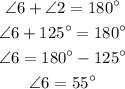
And since:
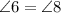
Then the measure iof angles 6 and 8 is 55°.
In summary the measure of each angle is: