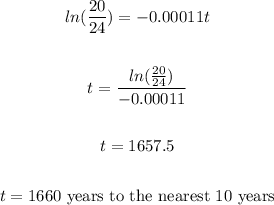Question

Please help! how long will it take 24g of plutonium-240 to decay to 20g? choose a,b,c or d?

Answer 1

Answer:

Step-by-step explanation:

The given equation is:

`Q(t)=Q_oe^(-kt)`

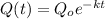
Quantity remaining after t years, Q(t) = 20 grams

The initial quantity, Q₀ = 24 grams

The decay constant, k = 0.00011

Substitute these parameters into the given equation and solve for t

`\begin{gathered} Q(t)=Q_oe^(-kt) \\ \\ 20=24e^(-0.00011t) \\ \\ (20)/(24)=e^(-0.00011t) \\ \\ \\ \end{gathered}`

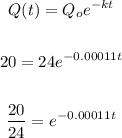
Take the natural logarithm of both sides

`\begin{gathered} ln((20)/(24))=-0.00011t \\ \\ t=(ln((20)/(24)))/(-0.00011) \\ \\ t=1657.5 \\ \\ t=1660\text{ years \lparen to the nearest 10 years\rparen} \end{gathered}`