Answer:
A. The graph is reflected across the x-axis and stretched vertically by
a factor of 2.
Explanation:
Transformations
For a > 0
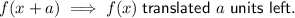

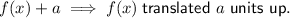


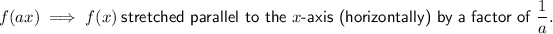

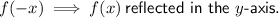
Given functions:
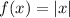
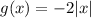
The series of transformations that take function f(x) to function g(x) are:
1. Reflection across the x-axis:
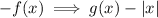
2. Vertical stretch by a factor of 2:
