Step-by-step explanation:
Consider the following figure:
By hypothesis, we have a Parallelogram ABCD with diagonal AC.
Now, since opposite sides of a parallelogram are congruent, we have:

and
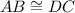
and by the reflexive Postulate of Congruency, we get:

Now, the Side-Side-Side Theorem states that if three sides of a triangle are equal to the corresponding sides of the other triangle, the two triangles are said to be congruent, we can conclude that:

Then, we can conclude that the correct answer is:
Answer:
Since opposite sides of a parallelogram are congruent, we have:

and
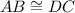
Now, by the reflexive Postulate of Congruency, we get:

then, by Side-Side-Side Theorem we can conclude that:
