Question

Two particles move along the x-axis. For 0 St<8, the position of particle P at time t is given byxp(t) = ln(t? - 2t + 10), while the velocity of particle Q at time t is given by vo(t) = 72 – 8t + 15.Particle is at position x = 5 at time t = 0.(a) Find the velocity function for particle P at time t.(b) For what time t is particle P at rest?(c) For 0 St S8, when is particle P moving to the left?(d) For what time t is particle Q at rest?(e) For 0

Answer 1

a) Vp = [(2t - 2)/(t² - 2t + 10)]

`Vp=(2t-2)/(t^2-2t+10)`

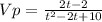
b) Particle P is never at rest.

c) The particle P moves towards the left from the time 0 ≤ t < 1.

d) The particle is never at rest in the time period given.

e)

Step-by-step explanation

Two particles P and Q are moving along the x-axis. For the time period between 0 ≤ t ≤ 8, the position of particle P is given as

Xp (t) = In (t² - 2t + 10)

while the velocity of Q is given as

Vq (t) = t² - 8t + 15

Particle Q is at position x = 5 at time t = 0

We should note that velocity is a time derivative of a particle's position and acceleration is a time derivative of a particle's velocity.

a) We are told to calculate the velocity for particle P at time t.

Velocity = (d/dt) (position)

Vp = (dXp/dt)

Xp (t) = In (t² - 2t + 10)

Vp = (d/dt) [In (t² - 2t + 10)]

To differentiate a function of a function, we first differentiate the sub function (t² - 2t + 10) then differentiate the parent function

`Vp=\frac{\text{dXp}}{\text{ dt}}=(2t-2)/(t^2-2t+10)`

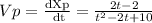
b) We are told to calculate the time period when the particle P is at rest, that is, when the particle P's position is at Xp = 0

Xp = In (t² - 2t + 10)

At rest, Xp = 0

In (t² - 2t + 10) = 0

Since In (1) = 0, we can say

In (t² - 2t + 10) = In (1)

t² - 2t + 10 = 1

t² - 2t + 9 = 0

We can then solve this quadratic equation using the quadratic formula and obtain two imaginary numbers showing that this particle P is never at rest.

c) For 0 ≤ t ≤ 8, when is the particle P moving to the left.

When the particle is moving to the left, then the velocity of the particle is negative.

Vp = [(2t - 2)/(t² - 2t + 10)]

When Vp is negative, Vp < 0

`\begin{gathered} (2t-2)/(t^2-2t+10)<0 \\ \text{Multiplying both sides by (t}^2-2t+10) \\ 2t-2<0 \\ 2t<2 \\ \text{Divide both sides by 2} \\ (2t)/(2)<(2)/(2) \\ t<1 \end{gathered}`

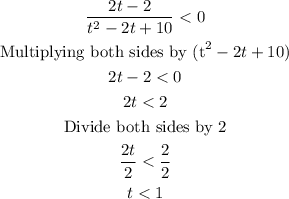
So, we can conclude that from the time 0 ≤ t < 1, the particle P moves towards the left.

d) For what time period is particle Q at rest.

To do this, we need to calculate the function for the position of particle Q at any time t.

Vq (t) = t² - 8t + 15

Xq = ∫ Vq dt

So, we just integrate the given function for the velocity of particle Q.

Vq (t) = t² - 8t + 15

Xq = ∫ Vq dt

= ∫ (t² - 8t + 15) dt

= (t³/3) - 4t² + 15t + c

where c is the constant of integration that can be solved by using the condition given that x = 5 when t = 0

Xq = (t³/3) - 4t² + 15t + c

when t = 0, Xq = 5

5 = 0 - 0 + 0 + c

c = 5

So,

Xq = (t³/3) - 4t² + 15t + 5

So, when particle Q is at rest, Xq = 0

Xq = (t³/3) - 4t² + 15t + 5

(t³/3) - 4t² + 15t + 5 = 0

We can then solve this polynomial to obtain the values of t.

Using the calculator,

t = -0.30748

t = 6.154 + 3.3035i

t = 6.154 - 3.3035i

Since none of the answers obtained are real and positive, the particle is never at rest in the time period given.

e) Find the time period 0 ≤ t ≤ 8, find the time periods that the two particles travel in the same directions.

For particle P, we know that from 0 ≤ t < 1, the particle travels to the left

And from 1 < t ≤ 8, the particle travels to the right.

For particle Q, we know that the the velocity is

Vq = t² - 8t + 15

When it's moving to the left, Vq < 0

t² - 8t + 15 < 0

(t - 3) (t - 5) < 0

We know that the solution of this inequality is 3 < t < 5

So, particle Q is moving to the left from 3 < t < 5

And moving to the right in the time periods t < 3 and t > 5

To recap,

Particle P moves to the left 0