Question

Add the rational expressions and type your answer in simplest form. When typing your answers, type your terms with variables in alphabetical order without any spaces between your characters. \frac{4}{x} + \frac{10}{y} The numerator is AnswerThe denominator is Answer

Answer 1

howe want to add the following

`(4)/(x)+(10)/(y)`

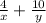
Notice that since both fractions have a different denominator, we cannot add them directly. what we will do is that we are going to multiply each fraction by a specific value, so we have that both fractions have the same denominator. Let us multiply the first fraction (from left to right) by y on both the numerator and the denominator. We get

`(4y)/(xy)`

and let us multiply the other fraction by x on both the numerator and the denominator. We get

`(10x)/(xy)`

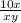
So we have the equivalent sum

`(4y)/(xy)+\text{ }(10x)/(xy)`

now, as both fractions have the same denominator, we can simply add the numerators to form the new fraction. So we have that

`(4)/(x)+(10)/(y)=(4y)/(xy)+(10x)/(xy)=(4y+10x)/(xy)`

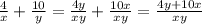
so the numerator of the result is 4y+10x and the denominator is xy