Question

Write a system of linear inequalities that defines the shaded region

Answer 1

a)

To solve a) we must find the equation of the two lines, let's say that f(x) is the equation of a line on the right, and g(x) is the equation of the line on the left. The inequation would be

`g(x)\le y\le f(x)`

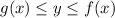
To find the equations here we can look that g(x) and f(x) are parallel, then they have the same angular coefficient, the function of f(x) would be

`f(x)=mx+b`

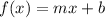
Looking at the graph we can see that b = 4, then

`f(x)=mx+4`

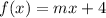
And we can use the fact that when x = 2 we have f(x) = 0, then

`0=m\cdot2+4\Rightarrow m=-2`

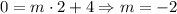
The function is

`f(x)=-2x+4`

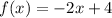
And for g(x), we just change +4 to -4, then

`g(x)=-2x-4`

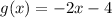
The inequation for the shaded area is

`\begin{gathered} g(x)\le y\le f(x) \\ \\ -2x-4\le y\le-2x+4 \end{gathered}`

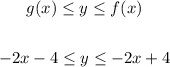
b)

For b) it's the same thing, find the line's equation, the system of inequations will be

[tex]\begin{cases}y\le f(x) \\ yWhere f(x) is the crescent function and g(x) the decreasing function.