We have to find the expression for x.
We have the relation:
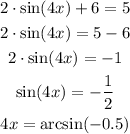
As the value of the sine function is negative, we can conclude that the angle 4x is placed in the 3rd or 4th quadrant:
The expression for this angle in the 4th quadrant can be written as:
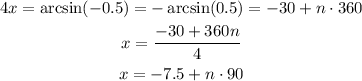
NOTE: We add n*360 to the value of 4x as all the angles that add a full circle to -30 will have the same value of the sine function.
If we express the the angle for the 3rd quadrant, we will have:
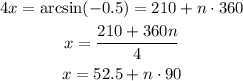
Then, the solutions for x are:
x = -7.5 + n*90
x = 52.5 + n*90