Given:
![\begin{gathered} Number(CDs)=1500 \\ Defective(CDs)=170 \end{gathered}]()
To Determine: The probability that the entire batch will be accepted if 6 CDs were randomly selected
Solution
![Non-defective(CDs)=1500-170=1330]()
Please note accepted CDs is the same as non-defective CDs.
If 6 were radomly selected without replacement, let us calculate the probability from the first to the sixth
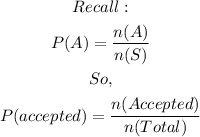
For the first accepted CD's
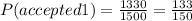
For the second accepted CD's without replacement
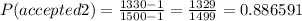
For the third CD's
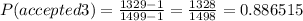
For the fourth Cd's
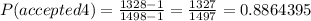
For the fifth Cd's

For the sixth CD's
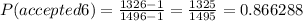
Therefore, the probability that the entire batch will be accepted would be

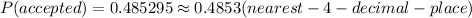
Hence, the probability that the entire batch will be accepted is approximately 0.4853