Question

Let x(t) = t ^ 3 - 4t ^ 2 + t and y(t) = t ^ 2 - 3t + 3

Answer 1

Given:

`\begin{gathered} x\left(t\right)=t^3-4t^2+t \\ y\left(t\right)=t^2-3t+3 \end{gathered}`

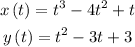
Required:

Find

`x(3),y(3),(dx)/(dt),\text{ }(dy)/(dt),(dy)/(dx)\text{ and speed at t=3}`

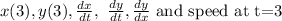
Step-by-step explanation:

The given functions are

`\begin{gathered} x\left(t\right)=t^3-4t^2+t \\ y\left(t\right)=t^2-3t+3 \end{gathered}`

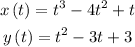
Substitute t=3 in x(t).

`\begin{gathered} x\left(3\right)=(3)^3-4(3)^2+(3) \\ =27-36+3 \\ =-6 \end{gathered}`

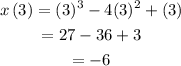
Substitute t=3 in y(t).

`\begin{gathered} y\left(3\right)=(3)^2-3(3)+3 \\ =9-9+3 \\ =3 \end{gathered}`

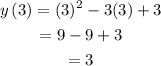
Differentiate the function x(t) with respect to t.

`(dx)/(dt)=3t^2-8t+1`

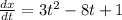
Substitute t = 3 in

`(dx)/(dt)`
`\begin{gathered} (dx)/(dt)|_(t=3)=3(3)^2-8(3)+1 \\ =27-24+1 \\ =4 \end{gathered}`

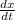
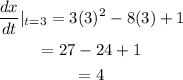
Differentiate the function y(t) with respect to t.

`\begin{gathered} (dy)/(dt)=2t-3 \\ (dy)/(dt)|_(t=3)=2(3)-3 \\ =6-3 \\ =3 \end{gathered}`
`\begin{gathered} (dy)/(dx)=((dy)/(dt))/((dy)/(dx)) \\ (dy)/(dx)=(2t-3)/(3t^2-8t+1) \\ (dy)/(dx)|_(t=3)=(2(3)-3)/(3(3)^2-8(3)+1) \\ =(3)/(4) \end{gathered}`

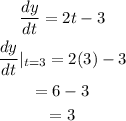
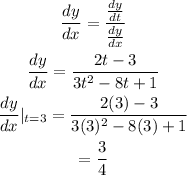
The speed at 3 is 3/4.

F