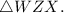Given YX congruent to ZX and WX bisecting
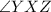 , triangles WYX and WZX are congruent by Side-Angle-Side (SAS) congruence, establishing equality in both sides and angles.
, triangles WYX and WZX are congruent by Side-Angle-Side (SAS) congruence, establishing equality in both sides and angles.
Statements and Reasons:
1. Given: YX is congruent to ZX.
- Reason: Given information.
2. Given: WX bisects angle YXZ.
- Reason: Given information.
3. Definition of Angle Bisector:
-
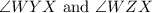 are formed by WX, the angle bisector of
are formed by WX, the angle bisector of
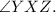
- Reason: By the definition of an angle bisector.
4. Side-Angle-Side (SAS) Congruence:
- YX is congruent to ZX (Given).
- WX is the common side.
-
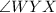 is congruent to
is congruent to
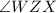 (Angle bisector).
(Angle bisector).
- Reason: Using SAS congruence.
5. Conclusion: Triangle Congruence:
-
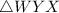 is congruent to
is congruent to
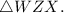
- Reason: From statement 4, triangles WYX and WZX are congruent by SAS congruence.
Therefore, the given conditions imply that
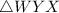 is congruent to
is congruent to