Question

One force acts westward on an object with a magnitude of 24.0 N; the other force acts southward with a magnitude of 18.0 N. Compose these two concurrent forces into their resultant.

Answer 1

30.0 N at 36.87 degrees southwest

Step-by-step explanation:

The forces are vectors, so we can represent the sum of these forces as follows:

Now, by the Pythagorean theorem, we can calculate the magnitude of resultant force:

`\begin{gathered} \text{ Resultant = }\sqrt[]{24^2+18^2\text{ }} \\ \text{ Resultant = }\sqrt[]{576+324\text{ }} \\ \text{ Resultant = }\sqrt[]{900} \\ \text{ Resultant = 30.0 N} \end{gathered}`

So, the magnitude of the resultant force is 30.0N.

Finally, we can calculate the angles as:

`\begin{gathered} \theta=\tan ^(-1)((18)/(24)) \\ \theta=\tan ^(-1)(0.75) \\ \theta=36.87\text{ degrees} \end{gathered}`

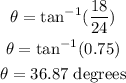
Then, the resultant force is 30.0 N at 36.87 degrees southwest