A) Notice that the trajectory of comet E corresponds to an ellipse whose major axis is parallel to the y-axis.
In general, the equation of an ellipse centered at (h,k) is
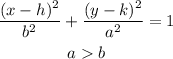
Then, in our case, the ellipse is centered at (0,-16), its semimajor axis length (a) is sqrt(400)=20, and its semiminor axis length is sqrt(144)=12.
Therefore, the vertices of the ellipse are
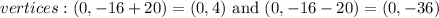
The answers to part A) are (0,-36) and (0,4).
B)
On the other hand, the equation of Comet H corresponds to a hyperbola whose transverse axis is on the y-axis. Therefore, its minimum distance to (0,0) is given by one of its vertices.
Calculate the vertices of the trajectory of comet H as shown below
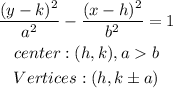
Thus, in our case,
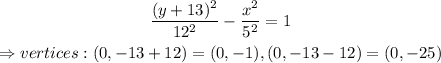
Comet H passes through (0,-1) which is at 1 unit from the origin.
On the other hand, the closest position of comet E from the sun is at its vertex (0,4).
The answer to part B is that comet H is closer to the sun at its maximum approximation point.
C)
In general, the foci of an ellipse/hyperbola are given by the formulas below
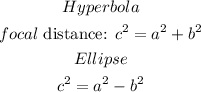
Then,

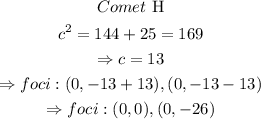
Thus, (0,0) (sun's position) is a focus of both comets.