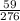Let C and D be the set of people who prefer cats and dogs respectively.
According to the given problem,
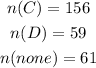
Note that mathematically, you can prefer one thing at a time. That means that none of the surveyed people will prefer cat and dog both,
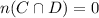
Then the total number of people surveyed is calculated as,
The probability of an event is given by,
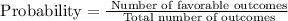
So the probability that a randomly chosen person will prefer dogs, is calculated as,
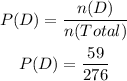
Thus, the corresponding probability is,