Question

Write a function f(t), the models the number of foxes in the population at t years after 2012, assuming a continuous growth rate.. f(t)=what is the fox population predicted to be in 2020?

Answer 1

It is given that the growth rate s 4%

The population in 2012 is 20040.

Recall the formula for the growth rate.

`Percent\text{ rate=}\frac{\frac{\text{present populaiton-past poulation}}{\text{past pulation}}*100}{\text{ the number of years}}`

`Percent\text{ rate=}((f(t)-20040)/(20040)*100)/(t)`

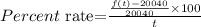
Substitute per cent rate =4 %, Present population =f(t) , the number of years and

Past population=20040 as follows:

`4=((f(t)-20040)/(20040)*100)/(t)`

`4t=(f(t)-20040)/(20040)*100`

`(4t)/(100)=(f(t)-20040)/(20040)`

`(4t)/(100)*20040=f(t)-20040`

`0.04t*20040+20040=f(t)`

`20040(0.04t+1)=f(t)`

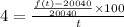
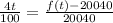
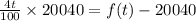
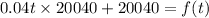
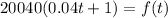
Hence the number of foxes in the population at t years after 20212 is

`f\mleft(t\mright)=(0.04t+1)20040`

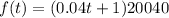
In the year 2020

The number of years after 2012 is =2020-2012=8

Substitute t=8 in the model f(t), we get

`f\mleft(8\mright)=(0.04*8+1)20040`

`f\mleft(8\mright)=(1.32)20040`

`f(8)=26452.8`

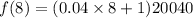
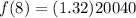
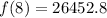
The number of foxes in the population predicted to be in 2020 is 26452.