Question

A bank's nominal annual interest rate is 5.8%. What is the effective annual interest rate if:(a.) interest is compounded monthly? Round your percentage to 4 decimal place accuracy.___%(b.) interest is compounded continuously? Round your percentage to 4 decimal place accuracy.___%

Answer 1

Part A. We are asked to determine the effective interest rate given the nominal interest rate. To do that we will use the following formula:

`r=(1+(i)/(n))^n-1`

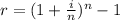
Where:

`\begin{gathered} r=\text{ effective interest rate} \\ i=\text{ nominal interest rate in decimal form} \\ n=\text{ number of compounding periods} \end{gathered}`

Now, since we are given that the interest rate is compounded monthly this means that the value of "n" is:

`n=12`

Now, the interest rate in decimal form is determined by dividing the interest rate by 100, like this:

`r=(5.8)/(100)=0.058`

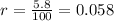
Now, we plug in the values:

`r=(1+(0.058)/(12))^(12)-1`

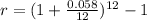
Now, we solve the operations:

`r=0.059567`

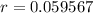
In percentage form is 5.9567%

Part B. If the interest rate is compounded continuously we use the following formula:

`r=e^i-1`

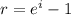
Plugging in the values we get:

`r=e^(0.058)-1`

Solving the operations:

`r=0.059715`

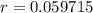
In percentage form we get 5.9715%