ANSWER:
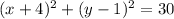
Center (4, -1), r = √30
Explanation:
We have an equation in its general form, we must convert it to its standard form of equation of the circle to determine the center and radius, like this:
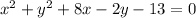
In the following way, we solve correctly

Center (4, -1), r = √30