Assuming the gas behaves as an ideal gas, we can use the Ideal Gas Law to calculate the pressure:
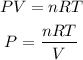
We need to use T in absolute terms, so we need to convert it to Kelvin:
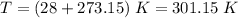
Since we have the volume in L and we want the pressure in atm, we can use the following unit for the R constant:
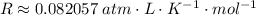
Using the these and the other given values:
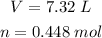
We have:

So, the pressure is approcimately 1.51 atm.