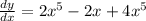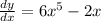ANSWER
dy/dx = 6x⁵ - 2x
Step-by-step explanation
The differentiation of a product rule is: given a function f(x) that is the product of two other functions g(x) and h(x):
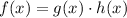
The derivative of f(x) is:
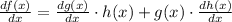
To find the derivative of y = x²(x⁴ - 1) first we have to identify which two functions are multipliying. Note that we have two polynomials multiplying, so the functions are:
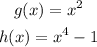
Find the derivatives:
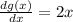
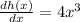
And replace into the formula for the product rule:
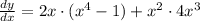
Apply some exponent rules to rewrite the expression:
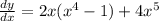
Also we can apply the distributive rule and express this result as a polynomial in standard form: