Answer:
(19.3, 20.1)
Explanation:
• Sample Mean = 19.7
,
• Sample Standard Deviation = 1.9
,
• Sample Size = 79
Since the population standard deviation is not known, we estimate it from the sample standard deviation and then use a t-students distribution to calculate the critical value.
The formula for estimating the population standard deviation is:
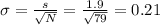
The degrees of freedom for this sample size is:
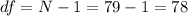
The t-value for a 95% confidence interval and 78 degrees of freedom is t=1.99.
Thus, the margin of error is:
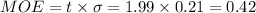
Thus, the lower and upper bounds of the confidence interval are:
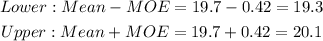
The confidence interval is (19.3, 20.1).