To find which of these lines are perpendicular, find the slope of each line.
To do it, use 2 points on the line and the following formula:
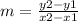
AB:
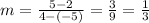
BC:
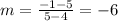
CD:
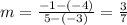
DA:
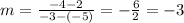
For 2 lines to be perpendicular, the product of their slopes must be -1. According to this the only pair that meets this condition is AB, DA.
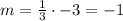
Segment AB and DA are perpendicular.