Solution
a)
To find the exponential growth function, we apply the exponential growth formula which is
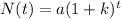
Where
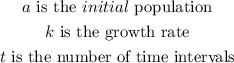
Given that
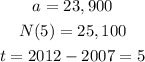
Substitute the variables into the exponential growth formula
![\begin{gathered} 25100=23900(1+k)^5 \\ \text{Divide both sides by 23,900} \\ (25100)/(23900)=(23900(1+k)^5)/(23900) \\ 1.05021=(1+k)^5^{} \\ \sqrt[5]{1.05021}=1+k \\ 1.00984=1+k \\ \text{Collect like terms} \\ k=1.00984-1 \\ k=0.00984 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wgpl7t93lzzef6t20x0p73xpsgox23kq6e.png)
Hence, the exponential growth function is
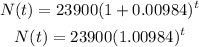
Hence, the exponential growth function is
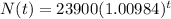
b)
For the population of the city in 2022,

Substitute for t into the exponential growth function
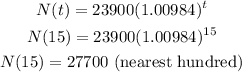
Hence, the population is 2022 is 27700 (nearest hundred)