ANSWER and EXPLANATION
To find the person with the larger paper, we have to find the area of both pieces of paper.
Jada's paper is a rectangular-shaped paper that measures 5 inches by 4 inches.
To find the area of the paper, we have to find the product of its side lengths.
The area of Jada's paper is:

Han's paper is shaped like the sector of a circle. The area of the sector of a circle is:
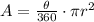
where θ = angle of the sector
r = radius
We have to find the measure of the angle of the sector by applying the formula for the length of an arc:
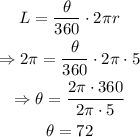
Hence, the area of Han's paper is:
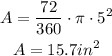
As we can see, Jada's rectangular piece of paper has an area that is greater than Han's piece of paper shaped like a sector. The area of Jada's piece of paper is 20 in² and the area of Han's piece of paper is 15.7 in²