Question

Pls make it fast I have other assignments.20 - 30 minutes on 1 question will be reported

Answer 1

Let it be:

• x: The larger number.

,

• y: The smaller number.

Then, we can write the following system of equations:

`\begin{cases}x+y=2\Rightarrow\text{ Equation 1} \\ 3x+2y=20\Rightarrow\text{ Equation 2}\end{cases}`

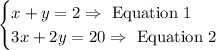
To solve the system of equations, we can use the elimination method.

Step 1: Multiply by -3 the Equation 1.

`\begin{gathered} -3(x+y)=2\cdot-3 \\ \text{ Apply the distributive property on the left side} \\ -3\cdot x-3\cdot y=-6 \\ -3x-3y=-6 \end{gathered}`

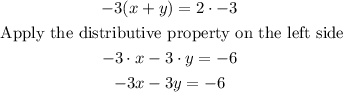
Step 2: We add both equations.

`\begin{gathered} -3x-3y=-6 \\ 3x+2y=20\text{ +} \\ --------- \\ 0x-y=14 \\ -y=14 \end{gathered}`

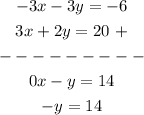
Step 3: We solve the resultant equation.

`\begin{gathered} \text{ Multiply by -1 from both sides} \\ -1\cdot-y=-1\cdot14 \\ y=-14 \end{gathered}`

Step 4: We replace the value of y in any of the initial equations. For example, in Equation 1. Then, we solve for x.

`\begin{gathered} x+y=2 \\ x-14=2 \\ \text{ Add 14 from both equations.} \\ x-14+14=2+14 \\ x=16 \end{gathered}`

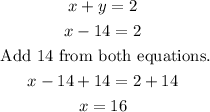
Therefore, the larger number is 16, and the smaller number is -14.