Question

Find a solution to the quadratic equation 4x2-5x+6=0

Answer 1

We need to solve the following equation:

`4x^2-5x+6=0`

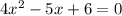
This is a quadratic equation, for which we can use the Baskhara equation to determine the roots. This equation is shown below:

`x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

If we replace the values on the equation, we will be able to determine both roots:

`\begin{gathered} x_(1,2)=\frac{-(-5)\pm\sqrt[]{(-5)^2-4\cdot4\cdot6}}{2\cdot4} \\ x_(1,2)=\frac{5\pm\sqrt[]{25-96}}{8} \\ x_(1,2)=\frac{5\pm\sqrt[]{-71}}{8} \\ x_(1,2)=\frac{5\pm i\sqrt[]{71}}{8} \\ x_(1,2)=(5\pm i8.43)/(8) \\ x_1=0.625+i1.05 \\ x_2=0.625-i1.05 \end{gathered}`

The solution to this equation is the pair of complex numbers: 0.625+i1.05 and 0.625-i1.05