Question

Math open ended question

Answer 1

The rough figure for the plot of the points is,

The obtained figure is parallelogram.

The formula for the area of parallelogram is,

`A=b\cdot h`

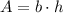
Here, b is base of parallelogram and h is height of parallelogram.

The dimension of base can be obtained by distance formula for two points on a cordinate plane. So obtain the distance between points (-4,2) and (3,-2) by using formula,

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

The height of parallelogram is equal to distance between base and its parallel line. So determine the vertical height between parallel side which is absolute value of change in y-coordinate.

Thus, for the area of parallelogram, base and height of parallelogram is required. Base is obtained by distance formula and height is equal to the chage in y-coordinate for the parallel side including the base.

Determine the length of base of parallelogram.

`\begin{gathered} b=\sqrt[]{(-4-3)^2+(-2+2)^2} \\ =\sqrt[]{49} \\ =7 \end{gathered}`

Determine the height of parallelogram.

`\begin{gathered} h=|-2-2| \\ =|-4| \\ =4 \end{gathered}`

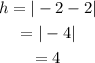
Determine the area of parallelogram.

`\begin{gathered} A=b\cdot h \\ =7\cdot4 \\ =28 \end{gathered}`

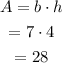
Thus area of figure obtained by joining the points is 28 square units.