Given:
The number of streetlights in a town is growing linearly
Let the number of streetlights = p
And the months = m
so,
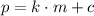
There were 143 lights 8 months ago; now there are 162 lights.
So, c = 143, m = 8, p = 162
So,
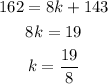
a) Write a linear model to describe the number of streetlights in the town over time, using months as the unit of time.
The linear model will be:
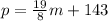
b) How many streetlights are expected a year from now? Round your answer to the nearest whole number.
So, m = 12
Substitute with m into the equation:
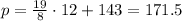
Rounding to the nearest whole number
So, p = 172
(c) When do you expect the number of streetlights to reach 240?
So, p = 240
Substitute with p to find m
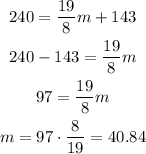
Rounding to the nearest whole number
So, the number of months = 41